本文基本上是老师的讲义, 少部分为自己理解或修改.
求最小 (大) 值问题
\begin{equation}\label{equ:OptPro}
\min_{x \in \R^n} f(x),\quad \underset{\text{(subject to)}}{\st} x \in X.
\end{equation}
其中:
- $n$: 维数;
- $x$: $x = (x_1, x_2, \cdots, x_n) \in \R^n$ 为 (优化) 变量;
- $f$: $\R^n \to \R$ 单值函数, 为目标 (函数);
- $X$: $X \subset \R^n$ 为约束集 / 可行域.
若 $X = \R^n$, 问题 \eqref{equ:OptPro} 变成了 $\displaystyle\min_{x \in \R^n} f(x)$ 称为无约束优化问题.
若 $X \subsetneq \R^n$, 则称为约束优化问题.
在很多情况下, 可以用一系列等式和不等式来约束:
\begin{equation*} x \in X \Longleftrightarrow \left\{\begin{array}{ll} c_i(x) = 0, & i = 1, \cdots, m,\\ c_j(x) \geqslant 0, & j = 1, \cdots, n. \end{array}\right.\end{equation*}在上述情况下, 问题 \eqref{equ:OptPro} 可以写成如下形式.
\begin{equation*} \min_{x \in \R^n} f(x),\quad \st \quad \begin{array}{ll} c_i(x) = 0, & i = 1, \cdots, m,\\ c_j(x) \geqslant 0, & j = 1, \cdots, n. \end{array}\end{equation*}- 若要求最大值, 可以将其化为最小值.
问题求解的复杂度取决于:
$n$ 的大小, 指数倍增长;
$f$ 与 $X(c_i, c_j)$ 的形式.
为什么关心优化问题的求解, 因为优化问题很重要, People optimize & Nature optimize. 比如说投资风险最小, 收益最大. 物理化学中希望出现在能量最小状态或熵最小状态.
一些例子
求解线性方程组
\begin{equation*} Ax = b,\end{equation*}其中 $A \in \R^{n \times n}$ 为对称正定矩阵, 求解 $x \in \R^n$. 在线性代数中已知
\begin{equation*} x = A^{-1}b = \dfrac{1}{\lrv{A}A^* b}.\end{equation*}但实际问题中 $n$ 的数量级为 $10^6 \sim 10^{10}$, $\lrv{A}$ 的算法复杂度为 $O(n!)$, 运算量极大, 需要转化为最优化问题.
构造
\begin{equation*} f : \R^n \to \R, \quad x \mapsto \dfrac{1}{2}x^\T Ax - b^\T x.\end{equation*}结论: 若 $x^* \in \R^n$ 是 $\displaystyle\min_{x \in \R^n} f(x)$ 的解, 则 $Ax^* = b$.
证明
\begin{equation*} 0 = \nabla f(x^*) = \left(\left.\dfrac{\pa f(x)}{\pa x_1}\right|_{x = x^* }, \cdots, \left.\dfrac{\pa f(x)}{\pa x_n}\right|_{x = x^* } \right),\end{equation*}其中
\begin{equation*} \left.\dfrac{\pa f(x)}{\pa x_i}\right|_{x = x^* } = \dfrac{1}{2}\left(Ax^* \right)_i + \dfrac{1}{2}\left(x^{* \T} A\right)_i - b_i = \left( Ax^* \right)_i - b_i = 0,\end{equation*}于是 $\left( Ax^* \right)_i = b_i$, $i = 1, \cdots, n$, 进而 $Ax^* = b$.$\square$
习题 1.1 已知 $Ax = \lambda x$, $\lambda \in \R$, $A \in \R^{n \times n}$ 对称正定, 想求 $A$ 的最小特征值 $\lambda_1$, 构造一个最优化问题与之相对应.
解 设
\begin{equation*} f(x) = \frac{x^\T Ax}{x^\T x},\quad x \in \R^n \setminus \lrb{0},\end{equation*}则 $f$ 的最小值为 $A$ 的最小特征值. 下面证明这个结论.
因为 $A$ 是实对称矩阵, 所以存在正交矩阵 $P$, 使得 $P^\T AP$ 是对角矩阵. 记该对角矩阵的主对角线上的元素为 $\lambda_1$, $\cdots$, $\lambda_n$, 不妨设其为从小到大的顺序 (交换 $P$ 的列顺序即可), 这些元素就是 $A$ 的特征值. $P$ 的列向量可以作为 $\R^n$ 的一组正交基, 记为 $x_1$, $\cdots$, $x_n$. $x$ 可以表示为 $x = \displaystyle\sum_{i = 1}^n \a_i x_i$, 有
\begin{align*}
x^\T Ax = (x, Ax) &= \left( \displaystyle\sum_{i = 1}^n \a_i x_i, A\left( \displaystyle\sum_{i = 1}^n \a_i x_i \right) \right) = \left( \displaystyle\sum_{i = 1}^n \a_i x_i, \displaystyle\sum_{i = 1}^n \a_i Ax_i \right)\\
&= \left( \displaystyle\sum_{i = 1}^n \a_i x_i, \displaystyle\sum_{i = 1}^n \a_i \lambda_i x_i \right) = \displaystyle\sum_{i = 1}^n \lambda_i \a_i^2 x_i^2 \geqslant \lambda_1 \displaystyle\sum_{i = 1}^n \a_i^2 x_i^2 = \lambda_1 x^\T x,
\end{align*}
其中 $(\cdot, \cdot)$ 表示内积. 于是 $f(x) \geqslant \lambda_1$, $x = \mu x_1$, $\mu \in \R \setminus \lrb{0}$ 时等号成立.$\square$
最优输送问题
有四个工厂需要用煤, 用煤量分别为 $F_1$, $F_2$, $F_3$, $F_4$. 有三个煤矿, 矿产煤量分别为 $M_1$, $M_2$, $M_3$, 满足
\begin{equation*} M_1 + M_2 + M_3 = F_1 + F_2 + F_3 + F_4.\end{equation*}设 $x_{ij}$, $i = 1, 2, 3$, $j = 1, 2, 3, 4$ 为 $i$ 矿到 $j$ 厂的运煤量, $d_{ij}$ 为 $i$ 矿到 $j$ 厂的距离, $c$ 为单位运费. 总运费为
\begin{equation*} f(x) = \sum_{i = 1}^{3}\sum_{j = 1}^{4} cx_{ij}d_{ij}.\end{equation*}最优化问题为
\begin{equation*} \min_{x = x_{ij}} f(x),\quad \st \quad \begin{array}{ll} \displaystyle\sum_{i = 1}^{3} x_{ij} = F_j, & j = 1, 2, 3, 4,\\ \displaystyle\sum_{j = 1}^{4} x_{ij} = M_i, & i = 1, 2, 3. \end{array}\end{equation*}可以将这个问题写成矩阵形式
\begin{equation*} \min_{x \in \R^{12}} \tilde{c}^\T x, \quad \st \tilde{A}x = \tilde{b}.\end{equation*}习题 1.2 写出该最优化问题中的向量 $\tilde{c}$, $\tilde{b}$ 以及矩阵 $\tilde{A}$.
解 设
\begin{equation*} x = \left( x_{11}, x_{12}, x_{13}, x_{14}, x_{21}, x_{22}, x_{23}, x_{24}, x_{31}, x_{32}, x_{33}, x_{34} \right)^\T ,\end{equation*}则有
\begin{align*}
\tilde{c} &= c \cdot \left( d_{11}, d_{12}, d_{13}, d_{14}, d_{21}, d_{22}, d_{23}, d_{24}, d_{31}, d_{32}, d_{33}, d_{34} \right)^\T ,\\
\tilde{b} &= \left( F_1, F_2, F_3, F_4, M_1, M_2, M_3 \right)^\T ,\\
\tilde{A} &= \begin{pmatrix}
1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0\\
0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1\\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1
\end{pmatrix}.\tag*{$\square$}
\end{align*}
人工神经网络
上图的人工神经网络构造了一个映射 $f : \R^2 \to \R$, $(x_1, x_2) \mapsto y$. 单个神经元如下图所示.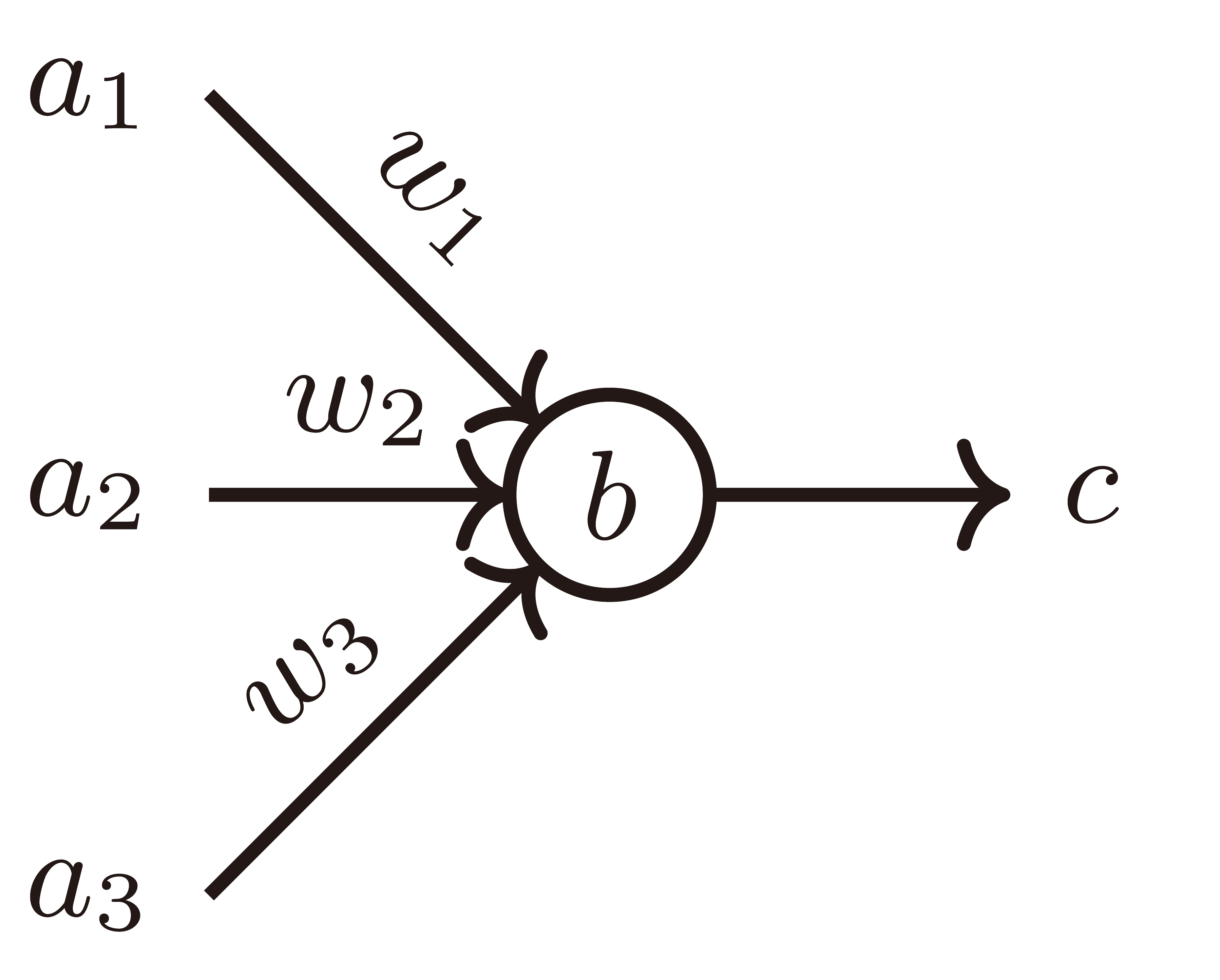
它的作用为
\begin{align*}
s &= a_1w_1 + a_2w_2 + a_3w_3 + b,\\
c &= \dfrac{1}{1 + \e^{-s}}\quad (\text{Sigmoid 激活函数}).
\end{align*}
习题 1.3 就上面这个简单的例子, 写出 $y = (x_1, x_2)$ 的显示形式.
解
\begin{align*}
y = \frac{1}{1 + \e^{-\left(\frac{w_7}{1 + \e^{-(x_1w_1 + x_2w_4 + b_1)}} + \frac{w_8}{1 + \e^{-(x_1w_2 + x_2w_5 + b_2)}} + \frac{w_9}{1 + \e^{-(x_1w_3 + x_2w_6 + b_3)}} + b_4\right)}}.\tag*{$\square$}
\end{align*}
如手写数字的识别, 将手写内容网格化成 $20 \times 20$ 的像素点, 若某个点被覆盖则取值为 $1$, 未被覆盖则取值为 $0$. 需要求解的函数为
\begin{equation*} h_{\bm w, \bm b} : \R^{400} \to \R^{10},\quad \bm \sg \mapsto \bm s,\end{equation*}其中 $\bm \sg$ 为手写内容, $\bm s$ 为 $0 \sim 9$ 数字的概率, $\bm w$, $\bm b$ 为神经网络的参数. 给一定数量的手写内容及相应的数字对神经网络进行训练, 如 $\left( \bm \sg_i, \bm s_i \right)_{i = 1, \cdots, 3000}$, 最优化问题为
\begin{equation*} \min_{\bm w, \bm b} \sum_{i = 1}^{3000} \lrvv{h_{\bm w, \bm b}\left(\bm \sg_i \right) - \bm s_i}_{l^2}^2,\end{equation*}求得的参数 $\bm w^*$, $\bm b^*$ 即为训练好的神经网络.
总结
将实际问题建模得到最优化问题, 设计算法去实现并分析, 求得最小 (大) 值.
可计算建模
算法与分析
